围观AMC10压轴题之一:AMC10的难度到底如何？

申请美国藤校，向来要求填写AMC10的成绩。这项比赛成绩因此也被誉为爬藤利器，其含金量应该不是浪得虚名。

有个小朋友，参加了今年11月6号的AMC10A卷考试。他说今年难度比较大，有不少题型没见过，计算量也比较大，考得不大好，因此准备重振旗鼓，再战下周的AMC10B卷。

AMC10的题型以灵活多变闻名，大多数都要结合几个知识点才能解答。周末备战，还试了试下面这道压轴题。

小朋友一向信心满满，不料这次一看题，直接大呼看不懂，真的很难吗？题目如下：
 

中文题意：S是一个边长为1的正方形。在此正方形的任意边上任意取两点，这两点之间距离最小为1/2的概率是（a-bπ）/c。a,b,c是正整数且最大公约数为1。求a+b+c=?

分析：看完题目是不是也有点懵？题目看上去并不难，就几行字。比起现在内地的数学考试一道题动不动就半页纸、不知道是考语文还是考数学的啰嗦题目，可谓叙述非常简单。

但是这题要读懂确实也不容易，仔细一看，发现文字说明虽少，却涉及几何，代数，概率，数论四个知识点。

四个知识点融合在一道题里面，难度和灵活度肯定不能低估，到底从哪下手？

思路：正方形有四条边，在任意边上任意取两个点，显然有好几种取法。可以两个点在同一条边上，也可以在相邻的边上，还可以在对面的边上。两点取在不同位置，两点之间距离的代数表达式就不同，对应的几何图形就不同，产生距离符合要求的概率也不同。

以上思路看出，要想直接得出一个代数表达式是不大可能了，只能试试分类讨论。

第一种情况：两点在同一条边上。

第二种情况：两点在相邻的边上。

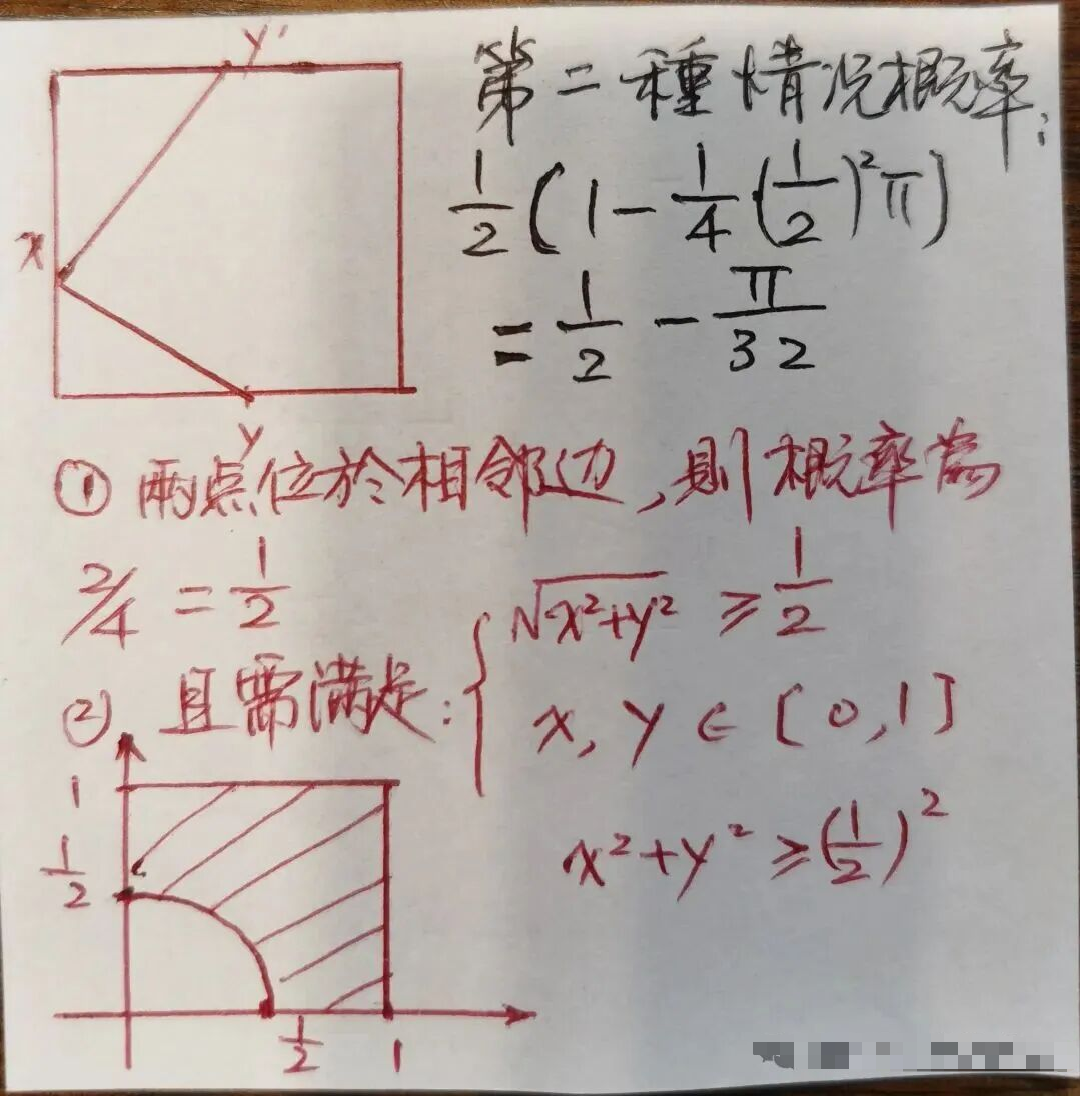
第三种情况：两点位于对面的边上。这种情况比较简单。如果位于对面边上，可能性为1/4，这种情况距离最小为1，最大为√2，全部大于1/2符合要求。因此第三种情况的概率就是1/4。

以上三种情况的概率相加，即：

1/16+（1/2-π/32）+1/4=（26-π）/32。即a=26，b=1，c=32。三者最大公约数为1，符合题意，且相加之和为59。

答案为A。

题目难度如何？欢迎讨论交流。